Proving 1+1=2 and other advanced theorems
What are numbers? What does it mean to add them? And why does a+b equal b+a? In this interactive session we’ll play the Natural Number Game to explore the foundations of math in Lean. Prerequisites: ability to count.
Motivation 1: can you convince a simpleton that a+b = b+a?
Imagine this dialogue between you and Simplicius the simpleton:
You:
2+3=3+2, wouldn’t you agree?Simplicius: Hmm, I don’t see it.
You: Okay,
2+3=5by calculation. And3+2=5by calculation. So both sides equal5.Simplicius: Okay, I see that. And it seems to work for some other examples.
You: Great. So you can see that, for any
aandb,a+b=b+a?Simplicius: Hmm, no, I don’t see that. How do you know?
You: ... C’mon, it’s obvious!
What can you say to Simplicius? Can you construct an argument that would convince him? That is, a proof?
But can’t we just say, “Simplicius is a rare idiot; let’s move on”? Let’s see a second example, which might be more familiar.
Motivation 2: convincing the computer your code is correct
You’ve written some code that gets the first number in an array:
function head(arr: number[]): number {
if (arr.length === 0) {
return -1;
} else {
return arr[0];
}
}Your type : number claims that this function always returns a number.
I’m convinced.
But annoyingly, the computer complains:

Stupid computer! Apparently it can’t see that, if the length of the array is not zero, there must be a value at the first index. Why not, and how can we prove it to the computer?
Our computers are like Simplicius.
We need a formal argument to convince it that arr[0] really is a number.
Lean
Enter Lean. In its own words:
Lean is a functional programming language [... and] a theorem prover.
How could this help us solve our problems above?
-
To help us show that addition is commutative, Lean gives us:
- A language to define what
a+b = b+areally means - A language to prove that claim
- A computer program to check that proof
- A language to define what
-
To help us show that our
headfunction is correct, Lean gives us:- A language to write our
headfunction - A language to prove that
headreally does always return a number - A computer program to check that proof
- A computer program to run or compile our
headfunction
- A language to write our
The natural number game
In this session we’ll play The Natural Number Game. Click it and you should see:
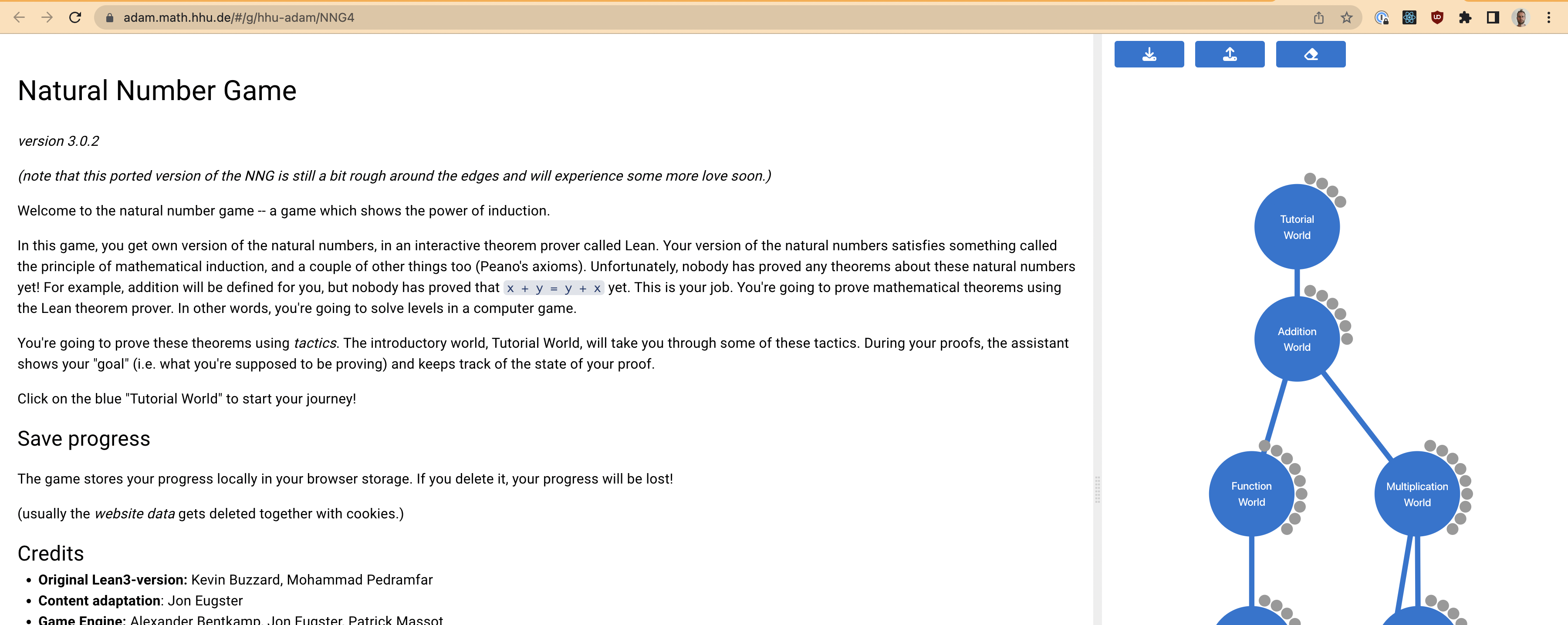
We’ll play the first 8 levels.
At the end, we will have proved that a+b=b+a.
1.1: rfl, reflection, “anything is equal to itself”
The most fundamental tactic, rfl!
Sounds useless, but it’s almost a definition of equality!
example ( x y z : ℕ ) :
x * y + z = x * y + z
:= by
rfl1.2: rw, rewriting, “If a=b, then you can replace a with b”
A problem from primary school:
What is the value of x? You might solve it by substituting:
This is exactly what the rw tactic does.
example ( x y : ℕ ) ( h : y = x + 7 ) :
2 * y = 2 * ( x + 7 )
:= by
rw [h]
rfl1.3: 0 and succ, defining the natural numbers
Above we vaguely referred to “numbers”, but for the rest of this session, we’re only going to be using the “natural numbers”, 0, 1, 2, 3, ..., denoted ℕ. Other kinds of “number” (e.g. negatives, fractions, reals, complex, ...) don’t exist in this session!
We’ve been writing numbers in decimal, e.g. 12.
But decimal is kinda complex,
so here we’ll work with a simpler notation:
125 = 1*(10^2) + 2*(10^1) + 5*(10^0)
0is a natural number.- If
nis a natural number,succ(n)is a natural number.
succ stands for “successor”.
You can interpret it as “The number after n”.
So instead of writing “3”, we instead write succ(succ(succ(0))).
Exercise: how would you write “7” in this notation?
Exercise: what number does succ(succ(succ(succ(0)))) represent?
Coders — you can think of the natural numbers as a linked list structure:
type Nat = 0 | { succ: Nat };
const three = { succ: { succ: { succ: 0 } } };Onto the exercise:
example ( a b : ℕ ) ( h : ( succ a ) = b ) :
succ ( succ a ) = succ b
:= by
rw [h]
rfl1.4: introducing addition
To convince anyone that “addition is commutative”, we first need to say what we mean by “addition”!
Here is how the Natural Number Game defines addition:
add_zero (a : ℕ) : a + 0 = a
add_succ (a b : ℕ) : a + (succ b) = succ (a + b)Or in English: “To calculate a+b,
repeatedly move the succs from b onto the outside,
until there are none left on b.
When there are none left, you have the total.”
Seeing this in action:
succ(0) + succ(succ(0))
= succ( succ(0) + succ(0) ) // add_succ
= succ(succ( succ(0) + 0 )) // add_succ
= succ(succ( succ(0) )) // add_zeroExercise: what numbers are we adding? And what is the result?
For the coders, here’s a rough equivalent in TypeScript:
function add(a: Nat, b: Nat): Nat {
if (b === 0) {
return a;
} else {
return { succ: add(a, b.succ) };
}
}example :
a + succ 0 = succ a
:= by
rw [add_succ]
rw [add_zero]
rflInterlude: induction
Imagine a chess board with a single bishop on one of the black squares. I then repeatedly move the bishop around (following normal rules: diagonal moves). What color square will the bishop be on after move 846,245?
Here’s an argument that it will be on a black square:
- At time
0, the bishop is on a black square. - If the bishop is on a black square at time
t, it must be on a black square at timet+1. This is because a diagonal move preserves the square color. - Therefore, the bishop is on a black square at all times
t. - In particular, it’s on a black square at time
846,245.
This is an argument by induction:
P(0)- If
P(n), thenP(n+1) - Therefore,
P(n)for all natural numbersn
2.1: zero_add and induction n
So, we have a + 0 = a.
We have it because we assumed it as an axiom that we called add_zero.
But what about 0 + a = a?
Looks very similar — but is it the same?
No!
It’s a separate claim, and we’ll call it zero_add.
Our task here is to prove it.
You could try using rfl or rw [h].
But you won’t get very far.
The final tactic you need is induction,
written induction n in Lean.
Here’s the induction argument in English:
-
If
a = 0, then0 + a = a.- Substitute and simplify to get
0 = 0, true by reflection.
- Substitute and simplify to get
-
Otherwise, assume
0 + a = a(the “induction hypothesis”).- Then we want to show
0 + succ(a) = succ(a). - Use
add_succto getsucc(0 + a) = succ(a). - Substitute the induction hypothesis to get
succ(a) = succ(a), true by reflection.
- Then we want to show
-
Therefore,
0 + a = afor all natural numbersa.
Here it is in Lean:
theorem MyNat.zero_add ( n : ℕ ) :
0 + n = n
:= by
induction n
rw [add_zero]
rfl
rw [add_succ]
rw [n_ih]
rfl2.2: add_assoc
From here, you don’t need to learn any new concepts!
The last three levels can all be solved with combinations of rfl, rw, and induction.
Good luck!
theorem MyNat.add_assoc ( a b c : ℕ ) :
( a + b ) + c = a + ( b + c )
:= by
induction c
rw [add_zero]
rw [add_zero]
rfl
rw [add_succ]
rw [add_succ]
rw [add_succ]
rw [n_ih]
rfl2.3: succ_add
theorem MyNat.succ_add ( a b : ℕ ) :
succ a + b = succ ( a + b )
:= by
induction b
rw [add_zero]
rw [add_zero]
rfl
rw [add_succ]
rw [n_ih]
rw [add_succ]
rfl2.4: add_comm
theorem MyNat.add_comm ( a b : ℕ ) :
a + b = b + a
:= by
induction b
rw [add_zero]
rw [zero_add]
rfl
rw [add_succ]
rw [n_ih]
rw [succ_add]
rflThis page copyright James Fisher 2023. Content is not associated with my employer.
 Granola
Granola